OO第一单元总结
前言
复杂度分析使用IDEA的 MetricsReloaded插件
代码规模分析利用IDEA的 static插件
UML类图使用IDEA绘图,再自行调整
任务概览
作业要求
- 作业1:根据形式化定义解析输入的表达式,输出恒等变形展开括号后的表达式。
- 作业2:形式化定义加入指数函数和自定义函数。
- 作业3:支持自定义函数嵌套并加入求导算子。
第一次作业
第一次作业为对包含幂函数与常数的表达式进行化简,涉及相对简单的嵌套,UML类图如下所示。
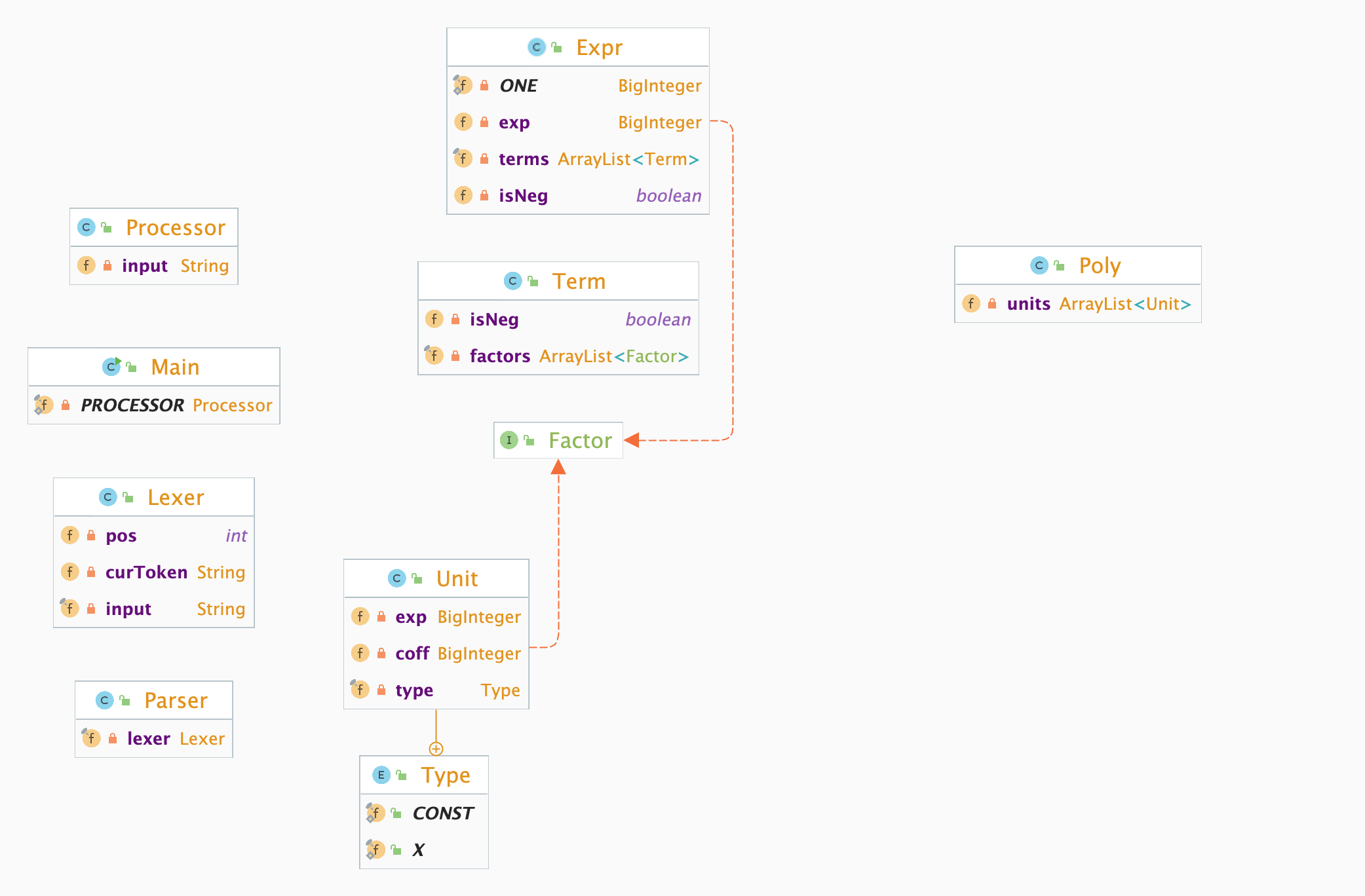
架构分析
通过分析 Expr与 Term的结构。我们不难发现,一个基本的 Expr可以看成又一个个基元构成,即
$$
Expr = \sum a \times x ^ b
$$
数据存储上,依照形式化表达设计为 Expr->Term->Factor。Parser和 Lexer作为工具类,分别承担句法分析和词法分析的功能。
值得注意的是,架构中事实上没有区分 Num和 Power,而是将其统一为 Unit类,存储一个形如$a \times x ^ b$的因子。
在读取和存储过程中,Parser和 Lexer合作,构建了一棵多叉表达式树。
Factor接口为因子类的公共接口,所有的因子都实现了这个接口,所有的非 Unit类通过 Poly,即多项式类进行运算,最后通过 Poly类调用 Unit类的 toString方法实现输出。
下图展示了这种读取和存储的过程的一个例子:
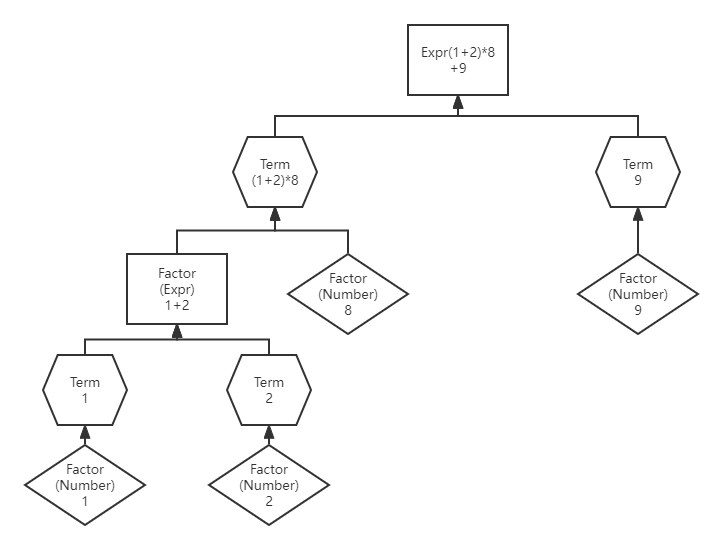
具体而言,获得答案的计算过程是和读取解析相解耦合的。在调用顶层 Expr对象的 extend()方法后,逐层向下调用 extend()方法,得到展开式。这其中,得益于 Unit类的统一性,每一层向上返回的都是一个 Unit对象的集合,达到了形式上和接口的统一。
复杂度分析
本次作业部分方法复杂度如下图,其余方法复杂度较低,未在图中体现。
可以看到,Parser中的 parseFactor()方法复杂度较高,分析原因知,设计该方法时对于常数和幂函数的解析都全部列在其中,没有分别抽象为分别的方法;Unit中的 toString()方法复杂度较高,为了优化输出的长度导致特判较多,复杂度较高。
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Parser.parseFactor() | 14 | 1 | 8 | 8 |
| Parser.parseExpr() | 8 | 1 | 6 | 6 |
| expr.Unit.toString() | 7 | 1 | 6 | 7 |
| Lexer.next() | 6 | 2 | 4 | 6 |
| expr.Expr.extend() | 6 | 2 | 6 | 6 |
| expr.Poly.toString() | 5 | 4 | 3 | 5 |
| expr.Term.extend() | 5 | 1 | 4 | 4 |
| Parser.parseTerm() | 4 | 1 | 4 | 4 |
| expr.Poly.multiUnit(Unit) | 4 | 1 | 3 | 3 |
| expr.Poly.Merge() | 3 | 1 | 3 | 3 |
| expr.Poly.adjustUnit() | 3 | 3 | 2 | 3 |
| expr.Poly.multiExpr(Poly) | 3 | 1 | 3 | 3 |
| Lexer.getNumber() | 2 | 1 | 3 | 3 |
| Parser.getExp() | 1 | 1 | 2 | 2 |
| Processor.treatPlusMinus() | 1 | 1 | 2 | 2 |
| expr.Poly.Negate() | 1 | 1 | 2 | 2 |
| Lexer.Lexer(String) | 0 | 1 | 1 | 1 |
| Lexer.peek() | 0 | 1 | 1 | 1 |
| Main.main(String[]) | 0 | 1 | 1 | 1 |
| Parser.Parser(Lexer) | 0 | 1 | 1 | 1 |
| Processor.adjustSign() | 0 | 1 | 1 | 1 |
| Processor.consumeBlank() | 0 | 1 | 1 | 1 |
| Processor.getString(String) | 0 | 1 | 1 | 1 |
| Processor.newInput(String) | 0 | 1 | 1 | 1 |
| Processor.outputString() | 0 | 1 | 1 | 1 |
| Processor.replaceDoubleStar() | 0 | 1 | 1 | 1 |
| expr.Expr.Negate() | 0 | 1 | 1 | 1 |
| expr.Expr.addTerm(Term) | 0 | 1 | 1 | 1 |
| expr.Expr.equals(Expr) | 0 | 1 | 1 | 1 |
| expr.Expr.setExp(BigInteger) | 0 | 1 | 1 | 1 |
| expr.Poly.Poly() | 0 | 1 | 1 | 1 |
| expr.Poly.add(Poly) | 0 | 1 | 1 | 1 |
| expr.Poly.createOne() | 0 | 1 | 1 | 1 |
| expr.Poly.unitMulti(Unit, Unit) | 0 | 1 | 1 | 1 |
| expr.Term.Negate() | 0 | 1 | 1 | 1 |
| expr.Term.addFactor(Factor) | 0 | 1 | 1 | 1 |
| expr.Unit.Negate() | 0 | 1 | 1 | 1 |
| expr.Unit.Unit(BigInteger) | 0 | 1 | 1 | 1 |
| expr.Unit.Unit(Type) | 0 | 1 | 1 | 1 |
| expr.Unit.canMerge(Unit) | 0 | 1 | 1 | 1 |
| expr.Unit.compareTo(Unit) | 0 | 1 | 1 | 1 |
| expr.Unit.getCoff() | 0 | 1 | 1 | 1 |
| expr.Unit.getExp() | 0 | 1 | 1 | 1 |
| expr.Unit.getType() | 0 | 1 | 1 | 1 |
| expr.Unit.merge(Unit) | 0 | 1 | 1 | 1 |
| expr.Unit.multiUnit(Unit) | 0 | 1 | 1 | 1 |
| expr.Unit.setCoff(BigInteger) | 0 | 1 | 1 | 1 |
| expr.Unit.setExp(BigInteger) | 0 | 1 | 1 | 1 |
Bug分析
本次作业没有出现bug。
在对room内其他同学互测时,发现两个bug:一个是没有处理$0$的输出;另一个是没有妥善处理表达式里的 \t和空格。
同时,我在此次作业中设计并实现了一个自动化评测机,这对检验程序的正确性有不小的帮助,也帮助我实现了hack,详细的分析将在评测部分介绍。
总结
“工欲善其事,必先利其器”
在写本次作业之初,我设计过很多架构,在设计阶段就推倒重来若干次。尽管在Pre中的冒险者游戏中已经我初步领会了面向对象的思想,但是面对较为抽象的表达式解析仍然显得捉襟见肘。
尽管如此,得益于 training部分提供的 Parser和 Lexer思路,我最终得以确定这个较为面向对象的设计。但是,这个架构依然存在相当的不足,在后面的迭代开发介绍中将会着重介绍。
第二次作业
相比于第一次作业,第二次作业新增了自定义函数与指数函数相关的内容,同时支持嵌套括号的解析。
相比第一次作业,增加了 Func类处理自定义函数,同时增加了 Exp类处理指数函数,UML类图如下:
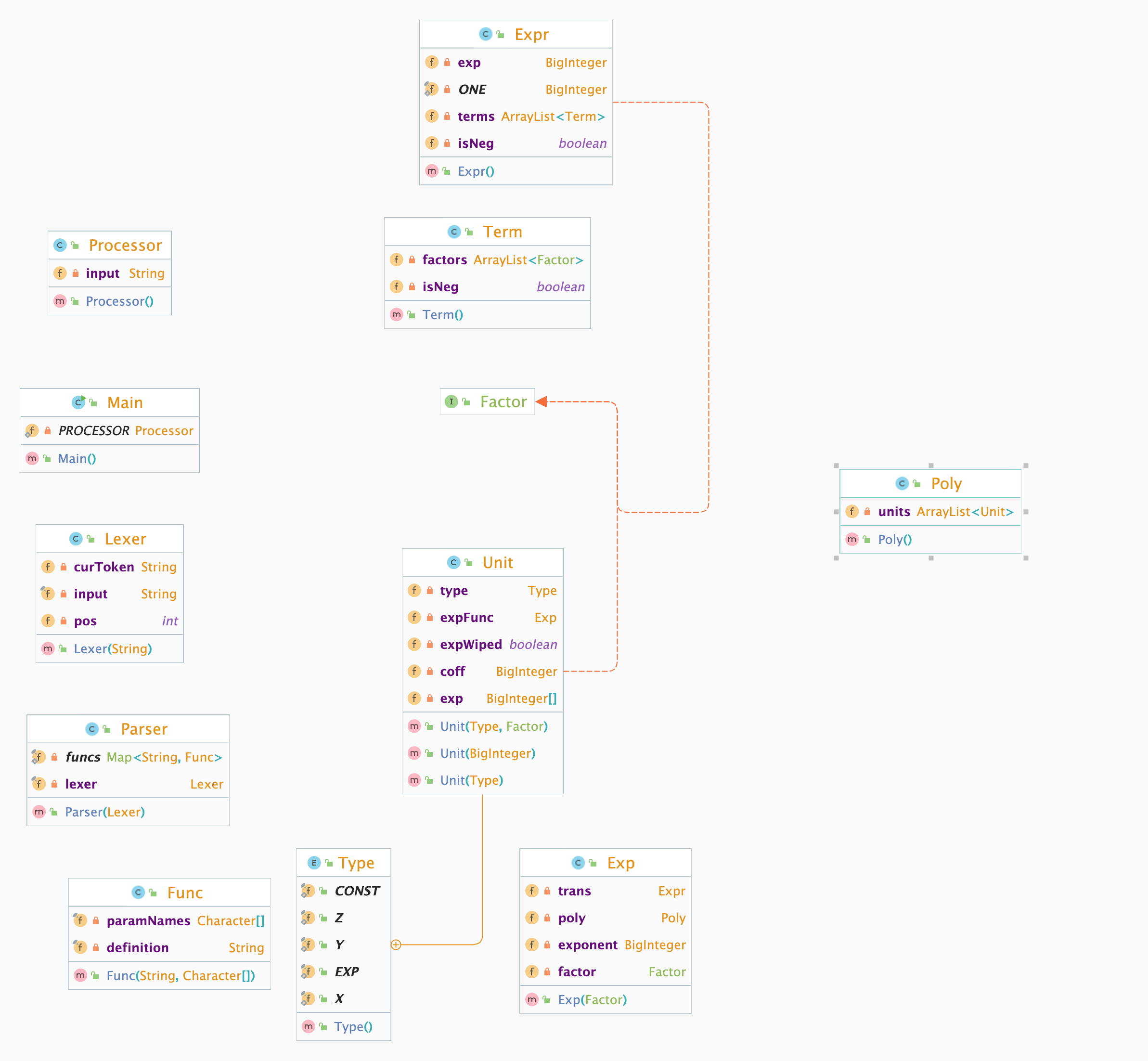
架构分析
相较于上一次作业以及未来的第三次作业,本次作业的工作量无疑是最大的,也难怪纪一鹏老师说这次作业很有可能会是本学期OO的难度巅峰。
对于本次作业的两个新增要求,我先完成了自定义函数的实现,再完成了指数函数的部分。
自定义函数部分
自定义函数分为两个部分,一是读入,二是调用。
有关读入,由于函数定义式依然符合我们的多项式语意,且定义式内不允许循环定义,故而直接沿用上一次的 Lexer和 Parser来解析。
有关调用,我在读入表达式时,就建立了参数与实参的Map,在解析时利用Map中的Map.Entry接口进行替换,效果不错,但是相较正则表达式替换的方法,虽然正确性上有保障,但是时间复杂度较高。
指数函数部分
通过分析本次式子可知,本次基元有所更新
$$
Expr = \sum a \times x ^ b \times exp(Factor) ^ c
$$
由于指数函数的特殊性,故我直接在初始化指数函数时直接将基元变形成如下式子,便于后续计算:
$$
Expr = \sum a \times x ^ b \times exp(Factor \times c)
$$
同样,我利用Poly类的 toString方法和String类的equals方法判断exp内的Factor是否相等,来进行后续合并。
复杂度分析
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Term.replace(HashMap<Type, Factor>) | 30 | 1 | 8 | 8 |
| Parser.parseFactor() | 19 | 1 | 12 | 12 |
| Unit.isSimple() | 11 | 7 | 9 | 15 |
| Unit.toString() | 11 | 1 | 9 | 10 |
| Unit.setExp(BigInteger) | 10 | 1 | 4 | 8 |
| Lexer.next() | 9 | 2 | 5 | 7 |
| Parser.parseExpr() | 8 | 1 | 6 | 6 |
| Unit.compareTo(Unit) | 8 | 7 | 7 | 8 |
| Exp.ifOne() | 7 | 5 | 2 | 5 |
| Expr.extend() | 6 | 2 | 6 | 6 |
| Poly.Merge() | 6 | 1 | 5 | 5 |
Func.invoke(List <Factor>) |
5 | 1 | 2 | 4 |
| Poly.toString() | 5 | 4 | 3 | 5 |
| Term.extend() | 5 | 1 | 4 | 4 |
| Parser.parseTerm() | 4 | 1 | 4 | 4 |
| Poly.multiUnit(Unit) | 4 | 1 | 3 | 3 |
| Poly.unitMulti(Unit, Unit) | 4 | 1 | 5 | 5 |
| Unit.multiUnit(Unit) | 4 | 1 | 4 | 5 |
| Unit.wipeExp() | 4 | 4 | 1 | 5 |
| Exp.Exp(Factor) | 3 | 1 | 3 | 4 |
| Exp.toString() | 3 | 1 | 3 | 3 |
| Poly.adjustUnit() | 3 | 3 | 2 | 3 |
| Poly.multiExpr(Poly) | 3 | 1 | 3 | 3 |
| Unit.Unit(Type) | 3 | 1 | 1 | 4 |
| Unit.replace(HashMap<Type, Factor>) | 3 | 3 | 3 | 4 |
| Exp.replace(HashMap<Type, Factor>) | 2 | 1 | 2 | 2 |
| Lexer.getNumber() | 2 | 1 | 3 | 3 |
| Parser.parseFuncDef() | 2 | 1 | 3 | 3 |
| Poly.isSimple() | 2 | 3 | 1 | 3 |
| Unit.clone() | 2 | 1 | 3 | 3 |
| Expr.clone() | 1 | 1 | 2 | 2 |
| Expr.pow(BigInteger) | 1 | 1 | 2 | 2 |
| Expr.replace(HashMap<Type, Factor>) | 1 | 1 | 2 | 2 |
| Main.main(String[]) | 1 | 1 | 2 | 2 |
| Parser.getExp() | 1 | 1 | 2 | 2 |
| Parser.parseFunc() | 1 | 1 | 2 | 2 |
| Poly.Negate() | 1 | 1 | 2 | 2 |
| Poly.clone() | 1 | 1 | 2 | 2 |
| Poly.pow(BigInteger) | 1 | 1 | 2 | 2 |
| Processor.treatPlusMinus() | 1 | 1 | 2 | 2 |
| Term.clone() | 1 | 1 | 2 | 2 |
| Exp.clone() | 0 | 1 | 1 | 1 |
| Exp.compareTo(Exp) | 0 | 1 | 1 | 1 |
| Exp.equals(Exp) | 0 | 1 | 1 | 1 |
| Exp.getExponent() | 0 | 1 | 1 | 1 |
| Exp.isSimple() | 0 | 1 | 1 | 1 |
| Exp.multExp(Exp) | 0 | 1 | 1 | 1 |
| Exp.pow(BigInteger) | 0 | 1 | 1 | 1 |
| Exp.setExponent(BigInteger) | 0 | 1 | 1 | 1 |
| Expr.Negate() | 0 | 1 | 1 | 1 |
| Expr.addExpr(Expr) | 0 | 1 | 1 | 1 |
| Expr.addTerm(Term) | 0 | 1 | 1 | 1 |
| Expr.equals(Expr) | 0 | 1 | 1 | 1 |
| Expr.setExp(BigInteger) | 0 | 1 | 1 | 1 |
| Func.Func(String, Character[]) | 0 | 1 | 1 | 1 |
| Lexer.Lexer(String) | 0 | 1 | 1 | 1 |
| Lexer.peek() | 0 | 1 | 1 | 1 |
| Parser.Parser(Lexer) | 0 | 1 | 1 | 1 |
| Poly.Poly() | 0 | 1 | 1 | 1 |
| Poly.add(Poly) | 0 | 1 | 1 | 1 |
| Poly.createOne() | 0 | 1 | 1 | 1 |
| Poly.isEmpty() | 0 | 1 | 1 | 1 |
| Processor.adjustSign() | 0 | 1 | 1 | 1 |
| Processor.consumeBlank() | 0 | 1 | 1 | 1 |
| Processor.getString(String) | 0 | 1 | 1 | 1 |
| Processor.newInput(String) | 0 | 1 | 1 | 1 |
| Processor.outputString() | 0 | 1 | 1 | 1 |
| Processor.replaceDoubleStar() | 0 | 1 | 1 | 1 |
| Term.Negate() | 0 | 1 | 1 | 1 |
| Term.addFactor(Factor) | 0 | 1 | 1 | 1 |
| Term.pow(BigInteger) | 0 | 1 | 1 | 1 |
| Unit.Negate() | 0 | 1 | 1 | 1 |
| Unit.Unit(BigInteger) | 0 | 1 | 1 | 1 |
| Unit.Unit(Type, Factor) | 0 | 1 | 1 | 1 |
| Unit.canMerge(Unit) | 0 | 1 | 1 | 1 |
| Unit.getCoff() | 0 | 1 | 1 | 1 |
| Unit.getExp() | 0 | 1 | 1 | 1 |
| Unit.getExpFunc() | 0 | 1 | 1 | 1 |
| Unit.getType() | 0 | 1 | 1 | 1 |
| Unit.merge(Unit) | 0 | 1 | 1 | 1 |
| Unit.pow(BigInteger) | 0 | 1 | 1 | 1 |
| Unit.setCoff(BigInteger) | 0 | 1 | 1 | 1 |
| Unit.setExpFunc(Exp) | 0 | 1 | 1 | 1 |
| Unit.setType(Type) | 0 | 1 | 1 | 1 |
可以看出,本次架构在Term类中实现自定义函数的替换部分的 replace方法复杂度极高,在Debug过程中,也同样是这个方法耗去了我大量的时间,可见越复杂,越易错!!!
Bug分析
本次作业没有出现bug。
在对room内其他同学互测时,发现两个bug:一个是对于exp的括号化简出错;另一个是自定义函数中exp函数替换出错。
在本次hack过程中,我着重查看了同屋同学代码架构的复杂程度进行了分析,对于明显架构复杂的代码进行hack,都得到了成功。
具体的hack方法则是利用cxc同学的评测机,对于可疑代码进行评测,得到错误输出后针对数据进行化简使其符合互测数据限制,最终hack成功。
总结
第二次作业是我在第一单元中花费时间最长的一次,尤其是指数函数的引入与化简合并,在Debug时给我造成了不小的困难,由于在完成本次作业时流感发烧,因此我在优化方面仅仅做了合并同类项和去exp函数的多余括号,但性能分上取得了 97.5分,可以说是十分侥幸的。同时,由于储存基元时采用了ArrayList,因此在合并同类项与Unit运算时被迫使用深克隆,而由于身体状态不佳,处于正确性考虑,我大量使用克隆,这也使我的程序运行时间大大增长。
第三次作业
本次作业引入了求导因子。本以为是最痛苦的一集,没想到成了最速的一集。UML类图如下所示:
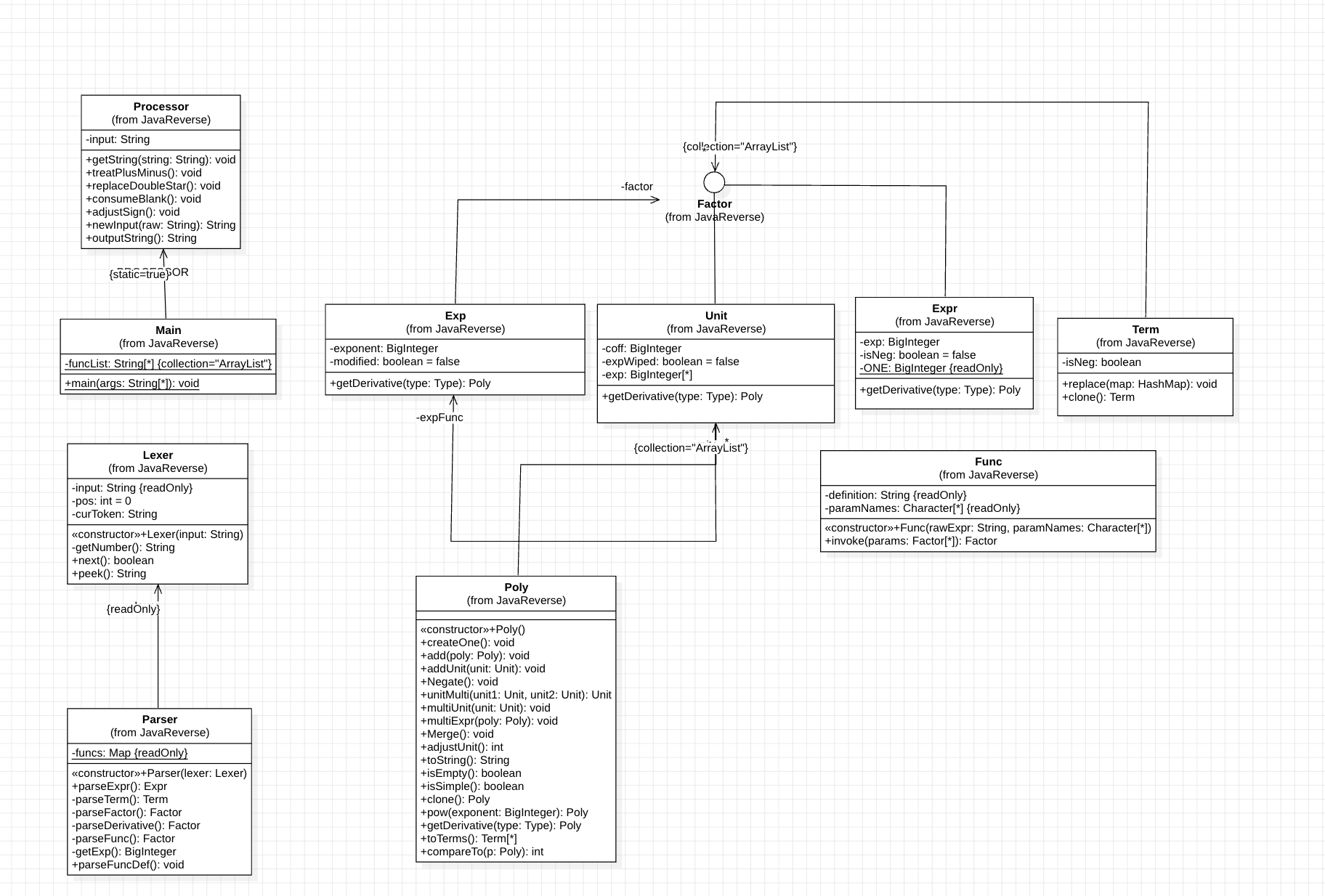
架构分析
与第二次作业相比,本次作业架构几乎没有发生变化,没有引入新的类。对于求导操作,与求字符串相似,在每一个相关的类中引入getDerivative()方法,返回Poly多项式类。对于带函数的求导,采用将自定义函数完全展开后再进行求导的方法。
复杂度分析
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Term.replace(HashMap<Type, Factor>) | 30 | 1 | 8 | 8 |
| Parser.parseFactor() | 20 | 1 | 13 | 13 |
| Unit.isSimple() | 11 | 7 | 9 | 15 |
| Unit.toString() | 11 | 1 | 9 | 10 |
| Lexer.next() | 10 | 2 | 6 | 8 |
| Unit.setExp(BigInteger) | 10 | 1 | 4 | 8 |
| Parser.parseExpr() | 8 | 1 | 6 | 6 |
| Unit.compareTo(Unit) | 8 | 7 | 7 | 8 |
| Exp.ifOne() | 7 | 5 | 2 | 5 |
| Expr.extend() | 6 | 2 | 6 | 6 |
| Poly.Merge() | 6 | 1 | 5 | 5 |
Func.invoke(List <Factor>) |
5 | 1 | 2 | 4 |
| Main.main(String[]) | 5 | 3 | 4 | 5 |
| Poly.toString() | 5 | 4 | 3 | 5 |
| Term.extend() | 5 | 1 | 4 | 4 |
| Parser.parseTerm() | 4 | 1 | 4 | 4 |
| Poly.multiUnit(Unit) | 4 | 1 | 3 | 3 |
| Unit.multiUnit(Unit) | 4 | 1 | 4 | 5 |
| Unit.wipeExp() | 4 | 4 | 1 | 5 |
| Exp.Exp(Factor) | 3 | 1 | 3 | 4 |
| Exp.toString() | 3 | 1 | 3 | 3 |
| Parser.parseDerivative() | 3 | 1 | 4 | 4 |
| Poly.adjustUnit() | 3 | 3 | 2 | 3 |
| Poly.compareTo(Poly) | 3 | 3 | 3 | 3 |
| Poly.multiExpr(Poly) | 3 | 1 | 3 | 3 |
| Unit.Unit(Type) | 3 | 1 | 1 | 4 |
| Unit.replace(HashMap<Type, Factor>) | 3 | 3 | 3 | 4 |
| Exp.clone() | 2 | 1 | 1 | 2 |
| Exp.replace(HashMap<Type, Factor>) | 2 | 1 | 2 | 2 |
| Lexer.getNumber() | 2 | 1 | 3 | 3 |
| Parser.parseFuncDef() | 2 | 1 | 3 | 3 |
| Poly.isSimple() | 2 | 3 | 1 | 3 |
| Unit.clone() | 2 | 1 | 3 | 3 |
| Unit.getDerivative(Type) | 2 | 1 | 3 | 3 |
| Exp.getDerivative(Type) | 1 | 2 | 1 | 2 |
| Expr.clone() | 1 | 1 | 2 | 2 |
| Expr.pow(BigInteger) | 1 | 1 | 2 | 2 |
| Expr.replace(HashMap<Type, Factor>) | 1 | 1 | 2 | 2 |
| Parser.getExp() | 1 | 1 | 2 | 2 |
| Parser.parseFunc() | 1 | 1 | 2 | 2 |
| Poly.Negate() | 1 | 1 | 2 | 2 |
| Poly.clone() | 1 | 1 | 2 | 2 |
| Poly.getDerivative(Type) | 1 | 1 | 2 | 2 |
| Poly.pow(BigInteger) | 1 | 1 | 2 | 2 |
| Poly.toTerms() | 1 | 1 | 2 | 2 |
| Processor.treatPlusMinus() | 1 | 1 | 2 | 2 |
| Term.clone() | 1 | 1 | 2 | 2 |
| Exp.compareTo(Exp) | 0 | 1 | 1 | 1 |
| Exp.equals(Exp) | 0 | 1 | 1 | 1 |
| Exp.getExponent() | 0 | 1 | 1 | 1 |
| Exp.isSimple() | 0 | 1 | 1 | 1 |
| Exp.multExp(Exp) | 0 | 1 | 1 | 1 |
| Exp.pow(BigInteger) | 0 | 1 | 1 | 1 |
| Exp.setExponent(BigInteger) | 0 | 1 | 1 | 1 |
| Expr.Expr() | 0 | 1 | 1 | 1 |
| Expr.Expr(Poly) | 0 | 1 | 1 | 1 |
| Expr.Negate() | 0 | 1 | 1 | 1 |
| Expr.addExpr(Expr) | 0 | 1 | 1 | 1 |
| Expr.addTerm(Term) | 0 | 1 | 1 | 1 |
| Expr.equals(Expr) | 0 | 1 | 1 | 1 |
| Expr.getDerivative(Type) | 0 | 1 | 1 | 1 |
| Expr.setExp(BigInteger) | 0 | 1 | 1 | 1 |
| Func.Func(String, Character[]) | 0 | 1 | 1 | 1 |
| Lexer.Lexer(String) | 0 | 1 | 1 | 1 |
| Lexer.peek() | 0 | 1 | 1 | 1 |
| Parser.Parser(Lexer) | 0 | 1 | 1 | 1 |
| Poly.Poly() | 0 | 1 | 1 | 1 |
| Poly.add(Poly) | 0 | 1 | 1 | 1 |
| Poly.addUnit(Unit) | 0 | 1 | 1 | 1 |
| Poly.createOne() | 0 | 1 | 1 | 1 |
| Poly.isEmpty() | 0 | 1 | 1 | 1 |
| Poly.unitMulti(Unit, Unit) | 0 | 1 | 1 | 1 |
| Processor.adjustSign() | 0 | 1 | 1 | 1 |
| Processor.consumeBlank() | 0 | 1 | 1 | 1 |
| Processor.getString(String) | 0 | 1 | 1 | 1 |
| Processor.newInput(String) | 0 | 1 | 1 | 1 |
| Processor.outputString() | 0 | 1 | 1 | 1 |
| Processor.replaceDoubleStar() | 0 | 1 | 1 | 1 |
| Term.Negate() | 0 | 1 | 1 | 1 |
| Term.addFactor(Factor) | 0 | 1 | 1 | 1 |
| Term.pow(BigInteger) | 0 | 1 | 1 | 1 |
| Unit.Negate() | 0 | 1 | 1 | 1 |
| Unit.Unit(BigInteger) | 0 | 1 | 1 | 1 |
| Unit.Unit(Type, Factor) | 0 | 1 | 1 | 1 |
| Unit.canMerge(Unit) | 0 | 1 | 1 | 1 |
| Unit.getCoff() | 0 | 1 | 1 | 1 |
| Unit.getExp() | 0 | 1 | 1 | 1 |
| Unit.getExpFunc() | 0 | 1 | 1 | 1 |
| Unit.getType() | 0 | 1 | 1 | 1 |
| Unit.merge(Unit) | 0 | 1 | 1 | 1 |
| Unit.pow(BigInteger) | 0 | 1 | 1 | 1 |
| Unit.setCoff(BigInteger) | 0 | 1 | 1 | 1 |
| Unit.setExpFunc(Exp) | 0 | 1 | 1 | 1 |
| Unit.setType(Type) | 0 | 1 | 1 | 1 |
| Unit.simpleClone() | 0 | 1 | 1 | 1 |
与第二次作业中复杂度较高的方法相同,原因一致。
Bug分析
本次作业在强测中未出现Bug,但是在互测中由于TLE中刀,原因正如我在第二次作业总结中写的那样——无脑克隆,而克隆方法本身需要递归,导致最终超时,这也是由于我个人的侥幸心理,认为互测数据不强,在明知有超时风险时,选择写OS作业,未进行优化。虽然强测侥幸过关,但是在互测中还是漏了马脚,果然还是这个道理。
She was still too young to know that life never gives anything for nothing, and that a price is always exacted for what fate bestows.
那时候她还太年轻,不知道所有命运馈赠的礼物,早已在暗中标好了价格。
——茨威格
总结
第三次作业不仅没有想象中可怕,还是三次作业中耗时最少的一次。得益于层次化结构的设计,新增求导运算的升级过程非常顺利,唯一的注意点是数学上的求导法则,需要在编码时严格遵守。只是可惜我的侥幸心理导致互测中刀,现在想来仍然感到深深可惜!!!
测试
本单元由于身体状况与个人时间的关系,只在第一次作业搭建了评测机,后续使用了cxc同学的评测机,这里再次感谢cxc同学!!!
在个人搭建评测机的过程中,我主要还是使用模拟递归下降的过程构建测试数据,并利用 Python中的 Sympy包来达到化简表达式并判断正误的效果,唯一的缺点是速度太慢。同时,我在构建评测数据时特意加入了诸如 x-x,+00000等数据,来保证随机生成数据的特殊性,但是只是可惜评测机hack效果不佳,更多还是靠手动构建数据。
心得体会
第一单元就这样痛并快乐地坚持了过去,但是和同学们投入的时间相比,我好像完成得还算轻松(?)
通过表达式解析的练习,我深刻体会了面向对象的设计思想,了解了递归下降的解析方法,初步尝试了层次化的类设计,这也为OS的Lab1提供了一些帮助。
最后还是感慨:设计为先,一个好的设计能为后续的编码工作省去不少麻烦;就比如,每次作业前,我都要花上一天半来进行设计,而不是基于上手编码,否则代码必然是漏洞百出。此外,还必须注重可扩展性,即在当前设计中打一个提前量,给未来可能引入的设计提前预留一些空间。
打个比方,我的程序在第一次就支持括号嵌套,第二次就支持自定义函数嵌套,现在第三次作业的程序还支持多变量运算与求导等等。
未来方向
总体而言,我认为课程组对于第一单元的设置已相对完备,但是第三次作业相较前两次明显过于轻松,我认为可以加入多变量运算与求导等要求。同样,我认为强测应该设置专门数据来卡时间复杂度,这样就能狠狠整治向我这样心存侥幸的同学!!!